[GNN] Machine leaning on graphs
그래프를 머신러닝에서 다룰 때 가장 큰 특이점은 각 노드들이 iid하지 않다는 것이다. iid (=independent and identically distributed) 하다면 각 노드가 독립적 (=독립적이라는 것은 각 노드가 다른 노드에 영향을 주지 않음을 의미한다) 이고 같은 확률분포를 가져야 하지만 각 노드는 서로 연결되어 있으므로 그렇지 않다.
이러한 점에서 일반적인 머신러닝 문제와 다르기 때문에, 풀고자 하는 문제의 도메인에 맞는 inductive bias (=일반화 성능을 높이기 위한 추가적인 가정, GNN에서는 순서 분별성이 있다) 를 필요로 한다.
또한 일반적으로 semi-supervised 문제이다. 테스트 노드의 라벨은 가려져 있지만 훈련 과정에서는 그래프 전체의 연결성을 활용하여 모델을 학습하여야 하기 때문에 라벨 정보가 없는 (unlabeled된) 테스트 노드의 라벨도 이용한다.
GNN에서 제시되는 문제들은 어느 영역을 예상하느냐에 따라 크게 node-level, edge level, graph level로 나뉜다.
Node level : Node classification
- SNS 상에서 봇을 탐지하는 문제
- citation graph, hyperlink 등 그래프에서 특정 문서의 주제를 예측하는 문제
그래프에 따라 homophily (=동종애, 라벨이 비슷한 노드들끼리 연결되어 있다) 또는 heterophily (=이종애, 라벨이 다른 노드들끼리 연결되어 있다) 인 경향성을 파악하여 모델을 설계한다.
Node degree : 노드에 연결되어 있는 edge의 개수 (how many neighbors a node has)
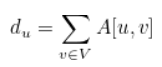
Node centrality : Node degree 식에 중요성 가중치를 추가 (how important a node`s neighbors are)
Node degree는 노드의 중요성을 설명하기에는 충분하지 않다. 노드의 이웃들의 중요성까지 고려한 지표가 Node centrailty이다. 아래의 식은 그래프의 인접행렬의 eigenvector을 찾음으로써 구할 수 있다.

Betweenness centrality : 다른 두 노드의 최단 거리에 해당 노드가 포함되어 있는 비율
(how often a node lies on the shortest path between two other nodes)
Closeness centrality : 다른 노드까지 도달할 수 있는 최단 거리의 평균
(average shortest path length between a node and all other nodes)
Clustering coefficient : 노드의 이웃들이 뭉쳐있는 정도 (how tightly clustered a node`s neighborhood is)
노드의 모든 이웃들 중에서 2개씩 고른 쌍 중에서 연결되어 있는 쌍의 비율로 계산한다.

실제 네트워크는 랜덤으로 생성된 네트워크보다 훨씬 높은 clustering coefficient를 가진다.
Graphlet degree vector (GDV) : 해당 노드에 대해 가능한 graphlet의 개수를 센 벡터
Edge level : Edge prediction
- 관계형 DB에서 새로운 정보를 파악하는 문제
- 약물의 부작용을 예측하는 문제
두 노드 사이의 관계를 예측하는 문제는 두가지 방법으로 접근할 수 있다.
1. 그래프에서 임의로 몇 개의 edge를 제거하고, 제거된 edge들을 예측하게 한다.
2. (그래프가 시간에 따라 변화하는 경우 : SNS, 교통 상황 등) 현재 시점의 그래프에서 다음 시점의 그래프를 예측하도록 한다.
Similarity matrix : 두 노드가 공유하는 이웃의 수를 행렬화 (number of neighbors that two nodes share)
두 노드가 연결되어 있을 가능도 (likelihood) 는 Silmilarity matrix에 비례한다. 공유하고 있는 이웃이 많을수록 가까이 위치할 것이고, 연결되어 있을 가능성이 높은 것이다.

Sorenson index : node degree의 합으로 나누어 정규화한다. 정규화하지 않으면 edge prediction task에서 node degree가 큰 노드로 예측이 집중될 것이다.

Salton index, Jaccard index : 마찬가지로, node degree가 미치는 영향을 최소화하면서 공유하는 이웃의 수를 측정한다.
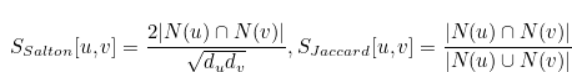
위의 방법론들을 local neighborhood overlap이라고 한다. local neighborhood overlap은 두 노드간의 거리가 3 이상이면 어떠한 경우에도 0이 나온다는 한계점이 있다. 따라서 좀 더 넓게 그래프를 보고자 등장한 개념이 아래에서 소개될 global neighborhood overlap이다.
Katz index : 두 노드 사이의 모든 길이에 대한 경로의 가짓수 (number of paths of all lengths between a pair of nodes)
인접행렬을 n번 제곱하면 이는 길이가 n인 경로의 수를 표현하는 행렬이 된다. β는 길이가 긴 경로에 대한 가중치이다. β가 1보다 크다면 긴 경로의 영향력을 높이고, 작다면 영향력을 낮춘다. 다만 이 방법또한 node degree에 영향을 크게 받는다.

Graph level : Graph classification/regression and Clustering
- 컴퓨터 프로그램의 데이터 흐름도를 보고 해당 프로그램의 악의성을 판단하는 문제 (graph classification)
- 분자 구조를 나타낸 그래프를 보고 해당 분자의 독성을 파악하는 문제 (graph regression)
- 전체 집단에 어떠한 커뮤니티들이 있는지 분석하는 문제 (clustering : community detection)
- 금융 거래 네트워크에서 사기 행각을 벌이는 그룹을 탐지하는 문제
각 그래프는 iid한 데이터로 인식되므로, graph-level task에서는 일반적인 머신러닝 방법론들을 적용할 수 있다.
그래프에서 유용한 특징을 어떻게 추출해내느냐가 중요한 부분이다.
Bag of nodes : 직역하면, node-level의 정보들을 가방에 담는다 (모두 모은다)
물론 node-level의 정보들은 지역적인 정보만 담기 때문에, graph-level의 정보를 표현하기에는 부족하다.
The Weisfeiler-Lehman kernel